
Dr. Amrita Bhattacharya
Associate Professor,
Dept. of Metallurgical Engg.
and Materials Science,
IIT Bombay, 400076, India
RESEARCH PROJECTS
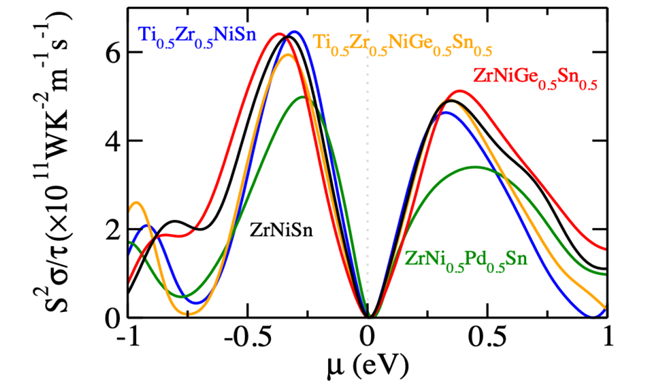
Charge and Heat Transport in thermoelectric materials
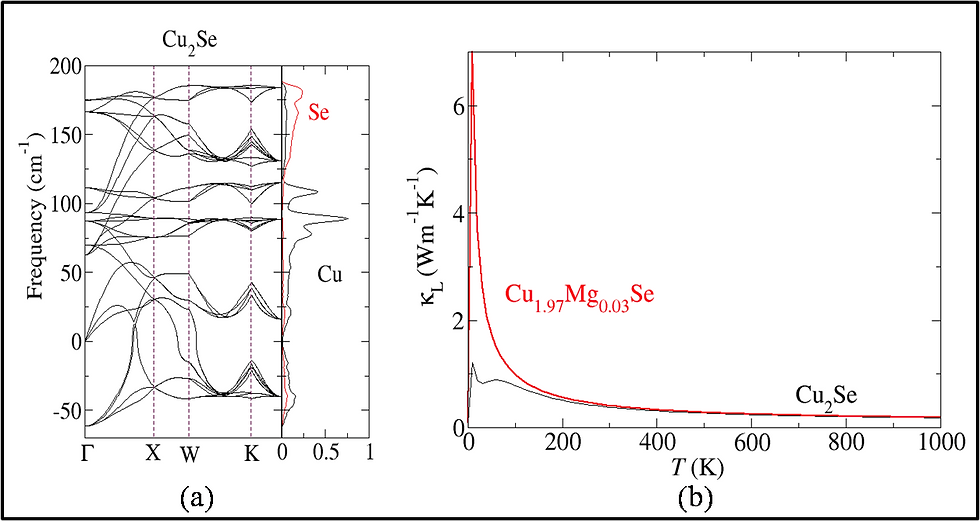
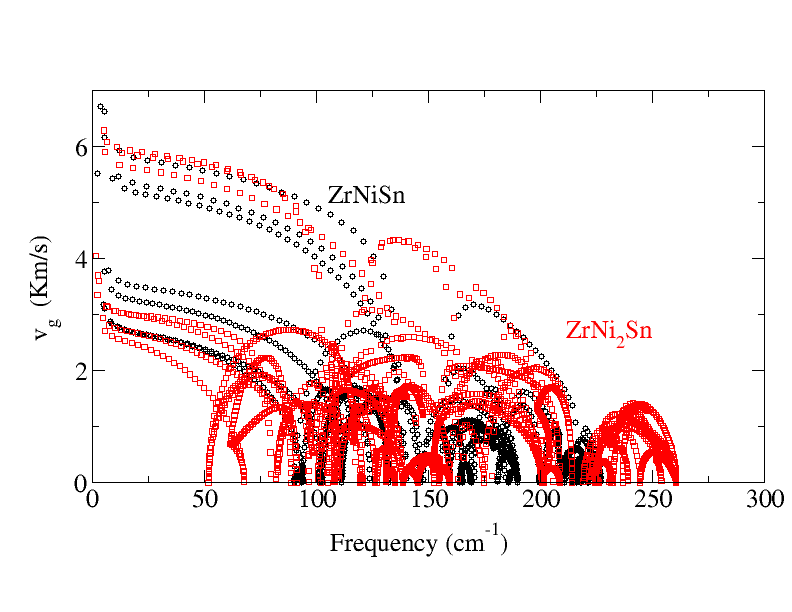
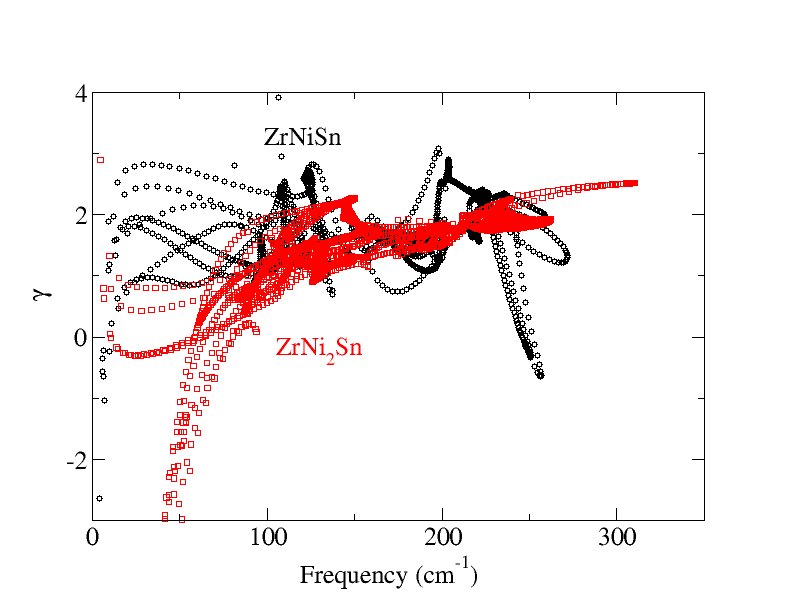
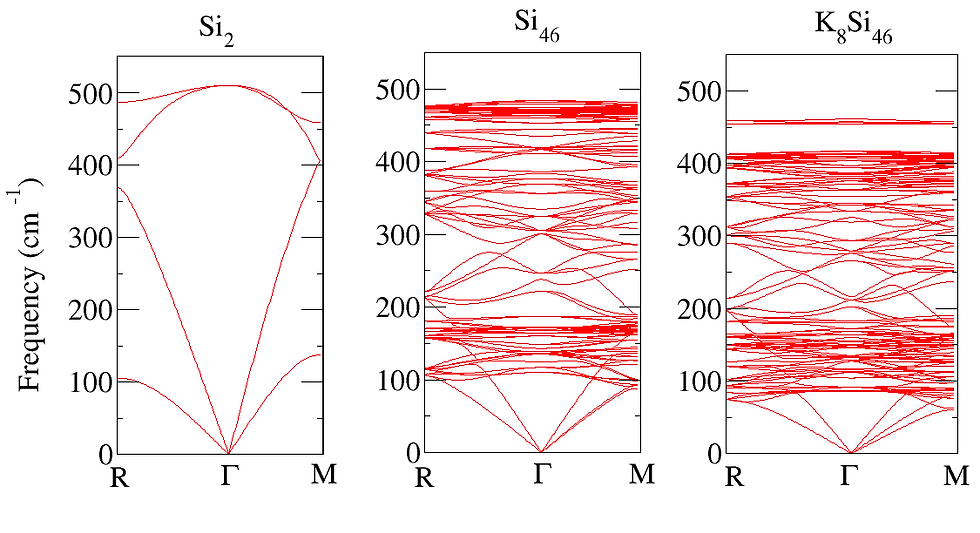
Thermoelectrics can be promising alternatives for the development of a green, sustainable and affordable energy economy. To date the efficiency of state-of-the-art thermoelectric materials is too low for their economically attractive deployment. The experimental design of improved thermoelectric materials is a tedious and costly task, since the efficiency depends both electrical as well as the vibrational properties, which inturn depend subtly on each other. Theory can aid to this. One can use Boltzmann transport equation (BTE) to calculate the lattice thermal conductivity , whereby phonon scattering lifetime can be either assumed constant [single relaxation time approach (SRTA)] or can be calculated using finite displacement method. Alternatively, the parameters, such as the Debye temperature, phonon group velocities, and Gr ̈uneisen parameters, of the acoustic modes can be extracted from the harmonic phonon band structure, to calculate the phonon-phonon scattering lifetimes. Using the scattering lifetimes in Debye Callway theory one can estimate the lattice thermal conductivity . Since, the assessment of the electron phonon scattering lifetime is more complicated than phonon phonon scattering (because they take place at much smaller time scale), BTE based methods are most simple and widespread to calculate the electronic transport coefficients i.e., the electrical conductivity , the electronic contribution to the thermal conductivity, and the Seebeck coefficient. In close analogy to BTE for phonon the electron phonon scattering lifetime can either be taken constant (SRTA) or can be calculated using perturbative approach.







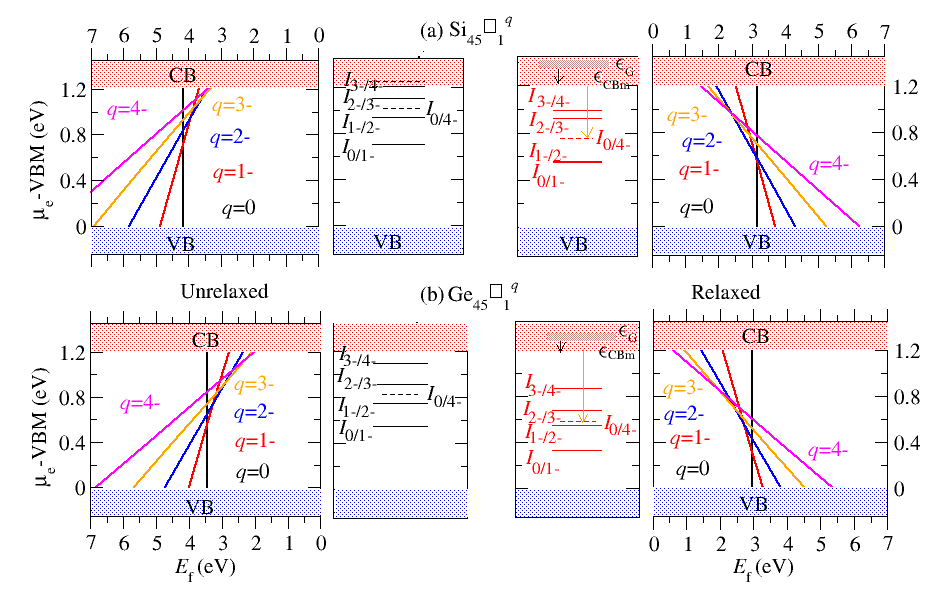
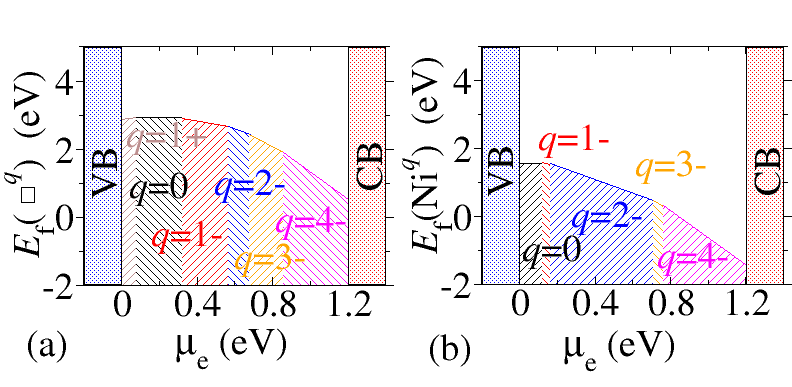
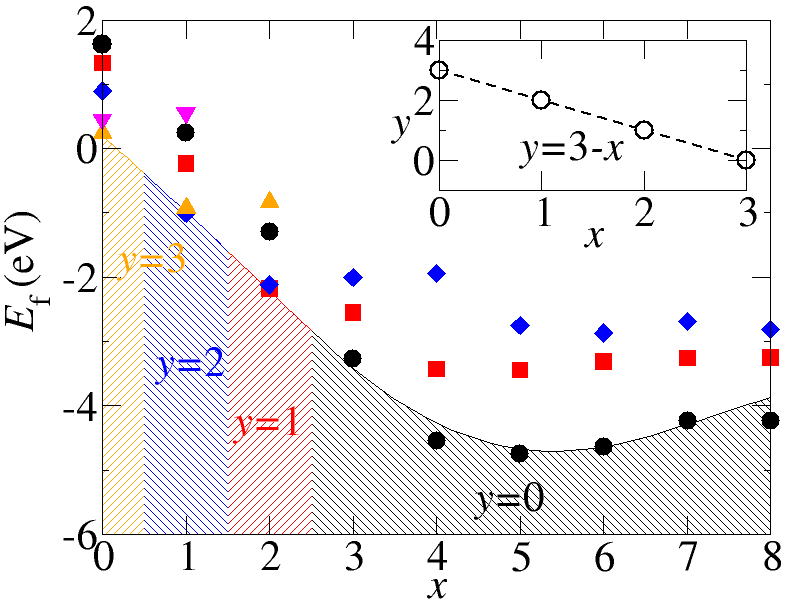
Modelling of Defects in Semiconductor
Point defects and impurities often play a decisive role in the physical properties of materials. Experimentally defect identification is typically difficult and indirect, usually requiring an ingenious combination of different techniques. First-principles calculations have emerged as a powerful approach that complements experiments and has become reliable enough to serve as a predictive tool. Using density density functional theory based methods one can calculate the defect charge states, charged defect formation energies, defect charge transition levels, thermodynamic stability of the defect etc. in semiconductor, configurational space diagram for calculating the optical transition levels etc.
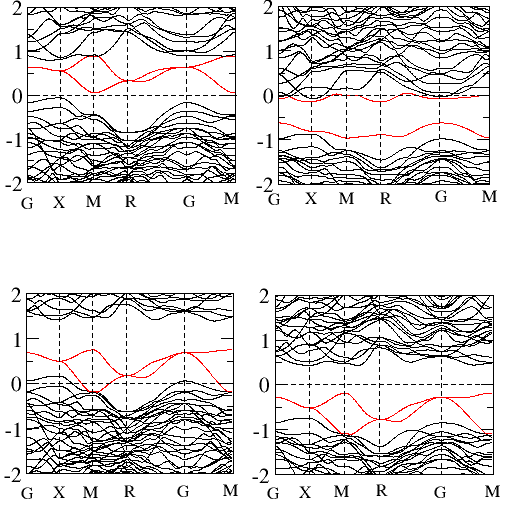




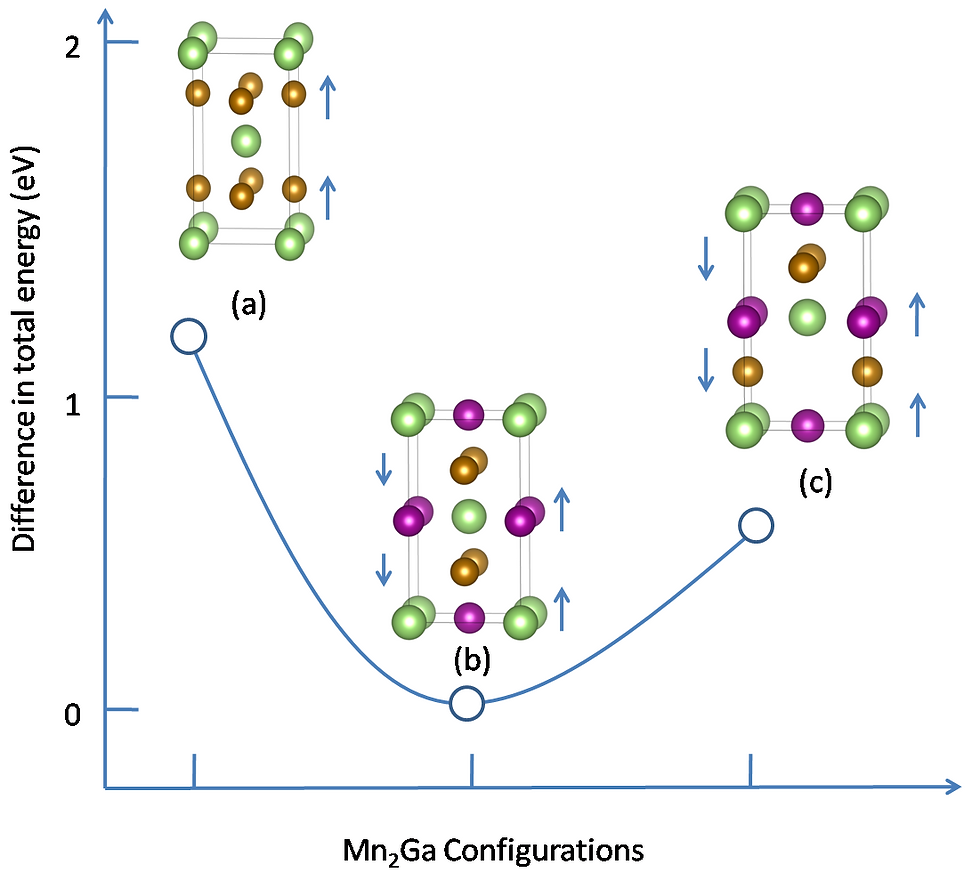
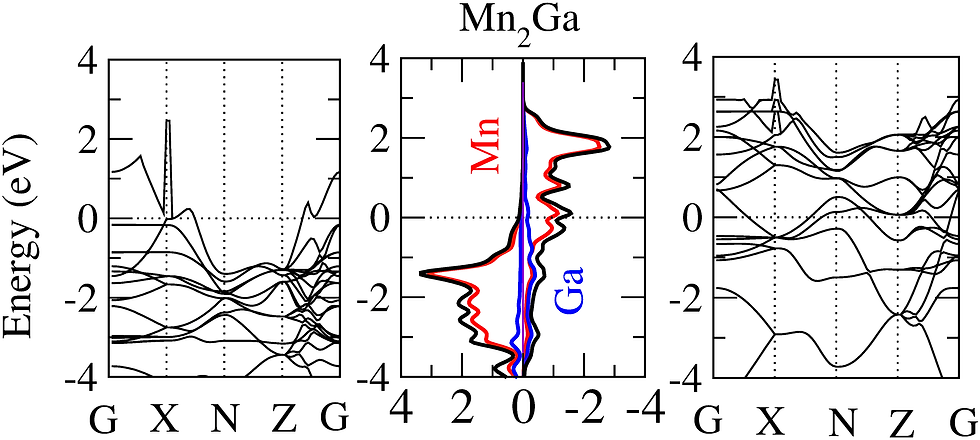
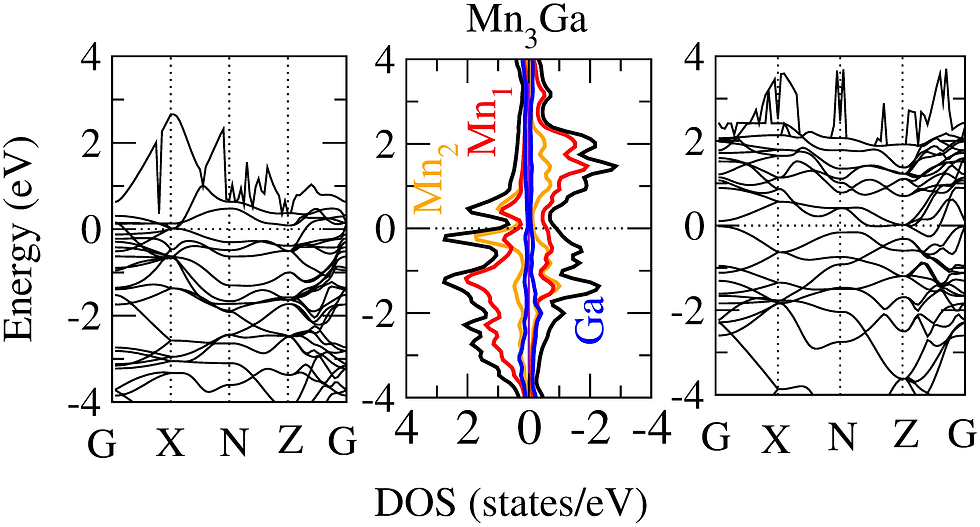
Magnetic structure in magnetic materials
For the last two decades, the permanent magnet industry is dominated by the rare-earth elements based magnetic materials. But the limited global supply of rare-earth elements has triggered the search of rare-earth free alternatives. The Mn based binary alloys such as Mn-Bi, Mn-Al, Mn-Ga, and Mn-Sb have aided to this search showing large magnetization, anisotropic constant, and high Curie temperature. Using density functional theory one can study the magnetic properties of these alloys from their spin polarized electronic structure, fat band, and Fermi surface plots etc. Furthermore, it is also interesting to study the effect of doping in the magnetic structure of these materials.



Quantum confinement effects in planar nanomaterials
Confining the dimension influences the properties and performance of the material, which are often found to be different from their respective bulk phases. Thus, the two dimensional planar nanomaterials such as Graphene, Silicene, BN sheet etc hold tremendous promise and enormous application potential for different fields. In particular, density functional theory based methods can be used to study the electronic, vibrational, mechanical, and optical properties of these planar nanomaterials for their application in the field of transistor based devices (due to anomalously high electric conductivity), hydrogen storage (due to large surface area), thin film coating (due to unusually high tensile strength) etc.

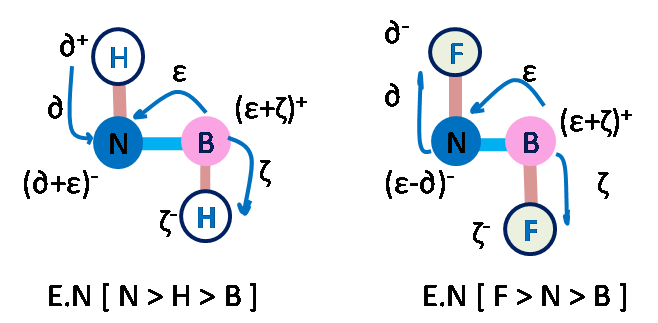
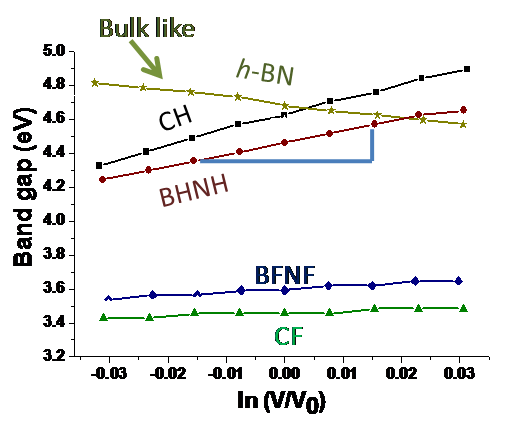
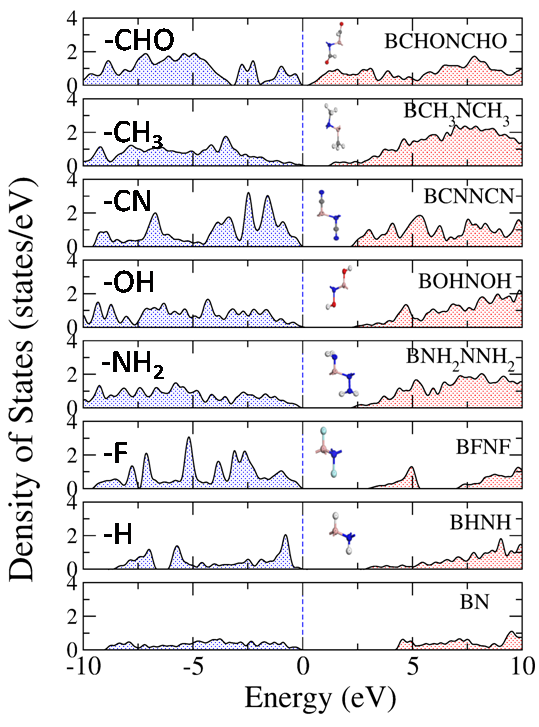




Machine learning the physical properties of materials
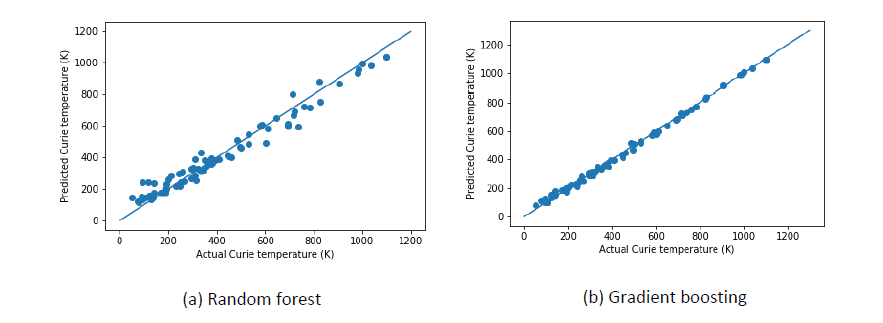
Extracting knowledge from data is rising as an enormously promising field within materials science. Designing materials through the effective use of data‐driven methods forms the core of the materials Genome project. The proposed project aims at developing a robust database containing the physical properties of a given compound class using first principles based DFT calculations and applying ML based methods to analyse the data and to predict hidden patterns. Several outcome may be expected; the proposed work will unravel the mechanism that governs the difference in properties of different compounds within the given material class. It will predict appropriate descriptors to the physical properties, so that the property of any unknown compound from the given compound class can be predicted.
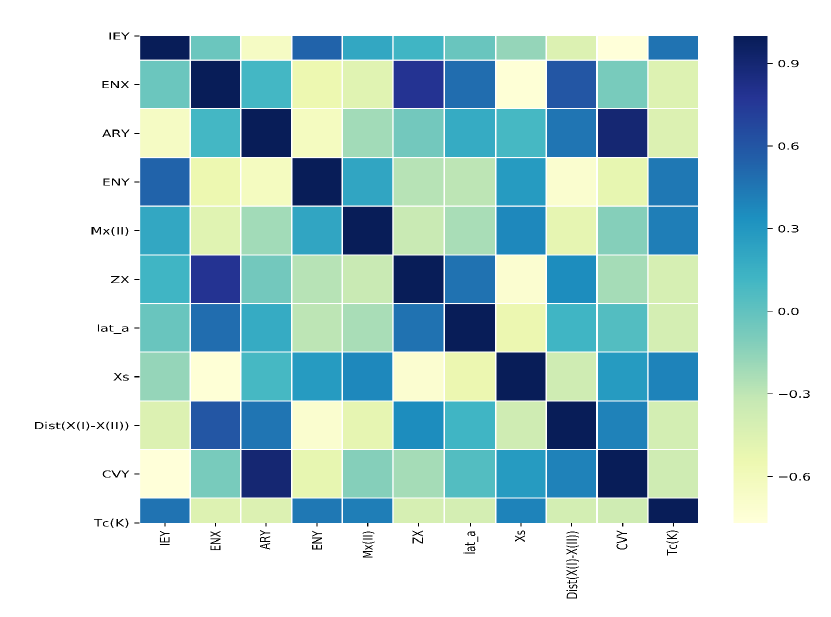
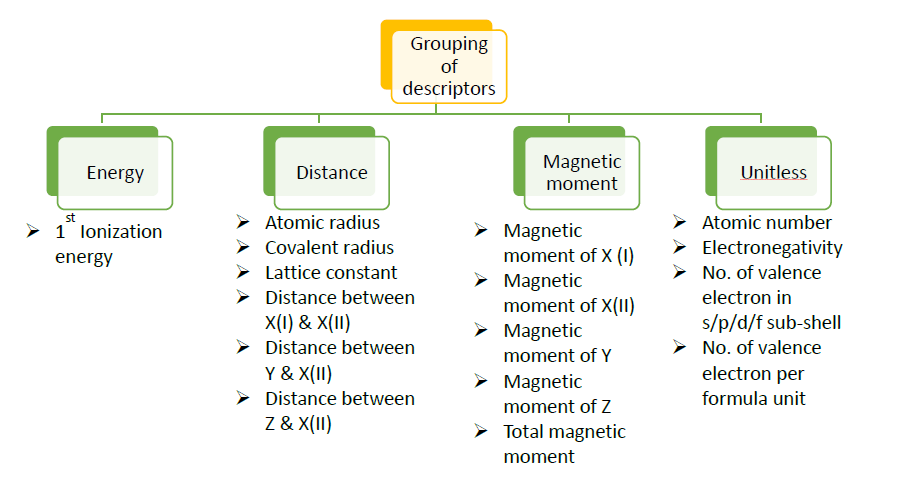



Method Developments
We do a lot of post processing in order to analyse the output obtained from an electronic structure code. Some of the examples are;
-
Coding to extract elemental and orbital contributions in electronic band structure.
-
Coding to extract group velocity, Gruneisen parameter etc from phonon band structure.
-
Coding to analyze the elastic constants of solid.
-
Integrating the lattice thermal conductivity of solid via different models.